スマホを使って三角測量ができるアプリを考えてみた。

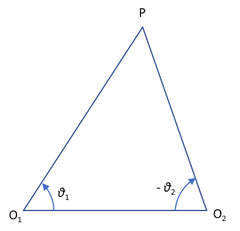
2点間の距離を図ろうと思うとしたとき、簡単な方法としては物指しだったり巻き尺で測るというやり方だろう。しかし現実には間に障害物があったりしてそういうやり方では測れないこともある。そんなときの代替手法のひとつが三角測量である。距離を測りたい対象物をPとして、基準になる地点O₁とO₂を選ぶ(上図)。このO₁とO₂の間の距離O₁O₂、角度θ₁、- θ₂がわかれば、三角形の合同の条件が成り立つので、△O₁O₂Pが確定する。あとはPまでの距離を計算すればいい。三角関数使って計算してもいいし、相似な三角形を描いて測ってもいい。今回は三角関数を使って計算した。

※上図で∠O₂の角度を - θ₂と書いたが、これはθ₁と逆向きであることをはっきりさせるためである。案外こういうところでつまずくことになる。

まず、2点間の距離は既知であるという前提※とする。

※巻き尺で測ってもいいし、事前に三角測量で測っておいてもいいし、とにかく何とかして距離を調べたという前提。今回は地図を使って調べている。これは事前に誰かが測定した結果を使わせてもらったというだけだ。

そうするとあとはθ₁ (= ∠O₁) とθ₂ (= ∠O₂)がわかれば点Pまでの距離が計算できる。角度を測る方法はいくつかあると思うが、今回はスマホのジャイロセンサーを使う。ジャイロセンサーはスマホの軸の周り(X、Y、Zの3軸)の回転速度ω (rad/s)を測定するものであり、一般的なスマホに搭載されている。このジャイロセンサーを使えば角度を測れる。具体的には、以下のように計算をする。

上図のようにジャイロセンサーの出力データがあるとする。ωというのは単位時間あたりにどれだけ角度が変わったかというものであるので、上のデータでi-1番目とi番目の間の角度の変化Δθ_i は

　Δθ_i = ω _i + ω _i+1 2 Δt

で近似できる。これを全データについて足し合わせていけば、計測開始してから何度角度が変化したかが計算できる(台形積分)。実際にスマホを90°回転させたときのデータと、角度を計算したのが以下である。

（どうやって90°回転させたかというと、部屋の角の壁にスマホの画面を当てて計測を開始し、次にもう一方の直角になった壁にスマホの画面を当てることで90°回転させた。）

※縦軸の単位が rad（またはrad/s）であることに注意。

上は建物の壁を使って90°回転させた方向にスマホを向けたが、三角測量の場ではどのようにスマホを向けるか？まず一番最初に考えるのは目線の先にスマホと対象物が一直線上に並ぶように向けるやり方だろう。ただこれだと、画面の向きが斜めになる可能性がある。スマホのジャイロセンサは画面の向きがどれだけ回転したかを計測しているので、画面が斜めを向いていると結果がずれてしまう。そこで今回はスマホのカメラをスコープ替わりにした。アプリ内にカメラのプレビュー画面を配置して、真ん中に十字線を描いた。プレビュー画面内に映った対象物をこの十字線に合わせてやれば、必ずスマホの画面を対象物に同じ角度で向けることができるという算段だ。

これでθ₁とθ₂を求めることができる。θ₁とθ₂が求まれば、あとは計算でO₁P、O₂Pが出せるはずだ。ではどうやって具体的に計算するか？結構単純で、連立方程式を解いてやるだけだ。

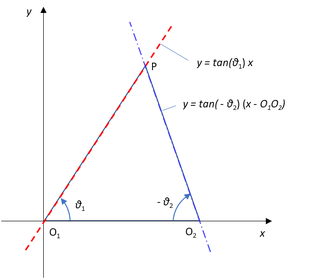
O₁を原点に、辺O₁O₂をx軸に一致させて先ほどの△O₁O₂Pをグラフ上に書くと上図のようになる。そうすると辺O₁Pは y = ax = tan(θ₁) xの直線上にあるし、辺O₂Pは y = b( x - O₁O₂) = tan(-θ₂) ( x - O₁O₂)の直線上にあることがわかる。点Pはこの2つ直線の交点にあたるので、この2つの連立方程式を解けば、Pの座標が求まるという算段である。

※直線の傾きをtanを使って表したが、tanが直線の傾きであることは、定義そのものからいえる。

この連立方程式を解くと

　x = tan(θ₂) tan(θ₁) + tan(θ₂) × O₁O₂

　y = tan(θ₁) tan(θ₂) tan(θ₁) + tan(θ₂) × O₁O₂

となる。

実際に作ってみたアプリの画面が下記。（デザインは、、、大目に見てください）

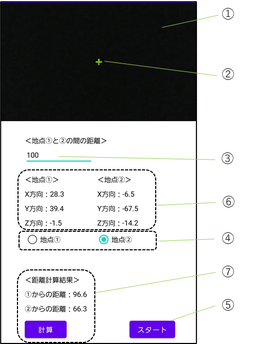
①カメラのプレビュー画面

②真ん中の十字線に対象物を合わせて角度計測を開始/終了する

③地点①(O₁）と地点②(O₂)の距離O₁O₂を入力する

④現在地(地点①または②)を選択する

⑤上のプレビュー画面で地点①（または②）を真ん中の十字合わせた状態でスタートを押す

　「スタート」が「ストップ」の表示に代わるのでスマホを回転させて、点Pを真ん中の十字線に合わせたら「ストップ」を押す。

⑥「スタート」を押してから「ストップ」を押すまでに回転した角度を表示。

　3つの軸の回転角を計算して表示してあるが、この後の計算で使うのはY軸の角度のみ。

　（地点①、②の違いは④で選択した現在地のこと）

⑦上記⑥までやって「計算」を押すと、地点①（または②）から点Pまでの距離が計算される

実際に使ってみて精度を検証してみた。鉄塔が見える開けた田んぼ地帯を選んで、点Pを鉄塔、O₁、O₂を農道の交差点にして計測した。

辺O₁O₂の距離は地図で確認すると110mなのでこの値を使用。次に角度θ₁、- θ₂を測定した結果、

　θ₁ = 103.6°

　- θ₂ = -66.2°

となった。これを使って鉄塔までの距離を計算すると

　O₁P = 567.2m

　O₂P = 602.7m

となる。地図で確認してみると、

　O₁P_（地図） = 589m

　O₂P_（地図） = 619m

のようなので、誤差数％(3～5％)といったところだろう。

今回誤差数％であったが、もっと精度よく測るにはどうしたらいいだろうか。

計算にはO₁O₂、θ₁、- θ₂の3つを使うが、それぞれが誤差にどれだけ影響するかまずは確認してみよう。

発生しうるちょっとしたずれで簡単に測定値が10％ほどずれることが分かった。

この誤差をどうやって小さくするか。

まずO₁O₂は今回は地図から距離を求めたが、地図上の点の選び方でずれが発生しそうだ。なるべく正確に点を選んで測るというのがまずは思いつくところだろう。もう一つ対策するとすれば、なるべくO₁O₂を長い距離にするということがありそうだ。点の選び方による誤差は地図の縮尺で決まるだろうから一定になるので、O₁O₂の距離を長くすれば、相対的に誤差が小さくなるという算段である。

次はθ₁、- θ₂の誤差をどうやって小さくするか。今回はスマホのカメラをスコープ替わりにしたが、それでもまだまだ誤差は発生しそうである。大きな要因としては手振れがあるが、対策としては三脚を使うことだろう。また計算上、角度が90°に近いと少しtanの値が大きくなるので、少し角度がずれただけで大きく変化してしまう。なので、なるべく鋭角になるように△O₁O₂Pを配置するのも対策になるだろう。（とはいえO₁O₂の距離を長くすることも限界があるだろうけども）

次は上記を対策してやってみようと思う。