「コンパス(3次元版 方針)」で計算の概要を説明したが、今回は実際に計算してみる。

 ※まずコンパス(3次元版 方針)に一度目を通してもらったほうが理解いただけると思う。

まずは磁場と加速度データを採取する。

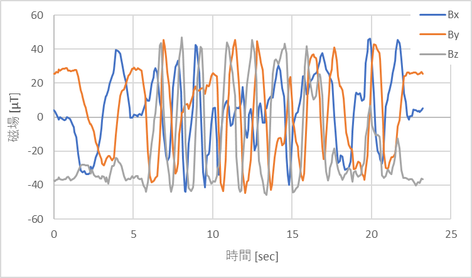
開始後5秒間くらいまでは水平にくるくる回し、その後いろんな方向に回した。

このデータを使うのだが、この後はこの中の1データを使って具体的に計算していき、適宜全体のデータがどうなってるか確認していこう。使うのは下記のデータにする。

 B = ( 9.54 , -20.13 , -38.20 )

 g = ( 0.80 , 7.45 , 3.50 )

Y軸方向に傾けた時のデータだ。

まずはスマホで計測した磁場Bからゼロ点のずれを差し引いたB_cを求める(センサー出力のズレを補正する)。

ゼロ点のずれはスマホをぐるぐる回転させた時のBx、 By、 Bzの各成分の(最大値+最小値)/2で求められる。今回のデータ(計測した全データ)で計算すると

　B_x : 1.18 μT

　B_y : 0.33 μT

　B_z : 0.48 μT

のずれであった。これをBから差し引けば補正後の磁場B_cが求まる。

 B_c = ( 8.36 , -20.46 , -38.68 )

※補正が正しかったかは磁場の絶対値が一定になっていることを確かめればいいのだが、今回はズレがほとんどなかったので割愛する。(元からほぼ一定だった)

次に座標変換するわけだが、そのためにはz軸の傾きθと回転軸nを求める必要がある。

まずはθ。重力加速度gとそのZ方向の成分のなす角度から求められるから、

cosθ = g_z /g

であり、

g_z = 3.50

g = √(g_x² + g_y² +g_z²) = 8.27

なので、

cos^ｰ1(3.50/8.27) = 64.95°

となる。

次にn。X-Y平面内の重力加速度の各成分のなす角度から求められて、

n = ( -  / g_x-y , g_x / g_x-y , 0)

で、

g_x = 0.80

g_y = 7.45

g_x-y = √(g_x² + g_y²) = 7.49

なので、

n = ( -0.99 , 0.11 , 0)

となる。

これをロドリゲスの回転公式に突っ込んでやれば座標変換できる。具体的な回転行列は割愛するが、計算すると、

B'_c = R_n(-θ) B_c

　 = ( 13.3 , 25.5 , -34.0)

となる。(具体的な回転行列はロドリゲスの回転公式で調べればすぐに出てくる。自分で書き下すと間違えそうなので、他サイトを見てほしい。)

この計算を他のデータにも適用してB'_c を計算したのグラフ。

X、Y方向は回転に合わせて磁場の大きさが変化しているが、Z方向の磁場はほとんど変化しておらず、35μTでほぼ一定になっている。座標系を水平にしているので、Z軸が一定になるのだ。狙い通り、XY面を水平にした座標系に変換できたようだ。

B'_c が求まったのでB'_c = (B'_cx , B'_cy , B'_cz)のうち水平方向の成分B'_ch = (B'_cx , B'_cy , 0)をスマホの座標系Xでの磁場B_chに変換してやる。

B'_ch = (B'_cx , B'_cy , 0)

　　= ( 13.3 , 25.5 , 0 )

であるので、これをもう一度スマホの座標系に変換してやる。つまり、

　B_ch = R_n(θ) B'_ch 

と計算すればよく、計算すると

　　　= ( 11.6 , 10.2 , -24.3)

となる。

他のデータについても計算したのが以下。

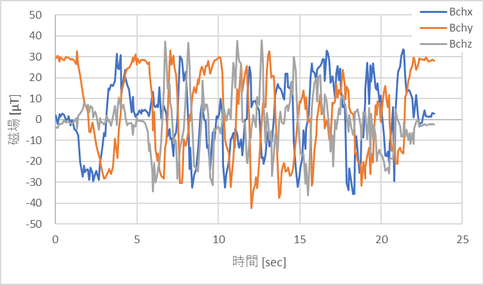
このB_chの絶対値(= √(B_chx² + B_chy² +B_chz²))を計算してやると、以下のようになり一定になる。(座標変換しただけなので当然と言えば当然の結果)

求めたB_chが地磁気の水平成分なので、このベクトルの向きが磁北を表している。このままでも磁北の向きは計算できているのだけれども、直行座標より極座標の方がもう少し直感的になるので計算してみる。

B_ch =  ( 11.6 , 10.2 , -24.3)　※直行座標

　　↓　座標変換

　　= ( r_p , θ_p , φ_p )　※極座標

　　=( 28.8μT , -57.5° , 41.1°) 

となる。画面斜め右上41°の方向、そこから57°画面奥側に向いていることになる。

すべてのデータに対してθ_pとφ_pを計算したのが以下。

グラフ化したところで直感的にはならなかったが、グラフをたどればどの瞬間にどの方向を向いていたかはわかるだろう。

一応検算。

下図のようにスマホを傾けて北に向けた場合。

B_ch = ( 32.0μT , -25.9° , 94.1°) 

磁北の方向はスマホから見たら潜った方向になりマイナス符号がついていて、また磁北はＹ方向に向いているのだが角度の基準はＸ軸なので90°近くになっていて、うまく計算できていそうだ。

同じ角度を保ってY軸を東→南→西とむけてみる。

東：B_ch = ( 32.2μT , -2.7° , 179.3°) 

南：B_ch = ( 31.6μT , 31.6° , -96.6°) 

西：B_ch = ( 31.5μT , -3.4° , 2.3°) 

東と西に向けた時はθ ～ 0°に近くなるが、これはZ軸と磁北が直交する形になるからだ。

※θはZ軸と鉛直方向の傾きではなくZ軸と磁北との傾きであることに注意。私は一瞬引っかかった。

向けた方向とθ_p、φ_pはちゃんと連動しているようなので計算は正しくできているようだ。

これでコンパスアプリに必要な計算はできた。あとは磁針をこの向きに向けて表示すればアプリは完成である。（どうやって表示させるかは割愛する）

磁気センサーと加速度センサーの出力から磁北の向きが計算できるようになった。

気になるのは、B_chの絶対値がほぼ一定にはなるものの、かなり大きくばらついているという点だ。これは恐らくスマホを回転させるときに重力加速度以外の加速度が加速度センサに乗ってきてしまうせいだろう。座標変換で使うθ、nの計算は重力加速度がどの方向に向いているかを使いたいので、それ以外の加速度が入ってきてしまうと計算がずれてしまうからだ。これを回避できないかと思って、加速度センサーの出力をスムージング（平滑化）してから計算してみたが、結果はぐちゃぐちゃになってしまいうまくいかなかった。スムージングしたのは重力加速度以外の加速度が加わると全体の加速度が変化するので、平滑化してその影響を排除できないかと考えたのだが、たぶん重力加速度の成分も平滑化してしまって結果がおかしくなったのではないかと思う。そうなると今の私にはゆっくり動かすことしかこのばらつきを抑える方法は思いつかない。まぁ、普通のコンパスアプリならそれで十分か。