コンパス(3次元 シンプルな方法)
「コンパス(3次元版 方針)」「コンパス(3次元版 実践編)」の2回に渡って3次元版のコンパスを作るためにどうやって計算しようとしたのかを書いた。そこでは座標変換してかなり複雑な計算をしたのだけれども、公開した後でもっとシンプルな方法があったことに気づいた。今回はそのシンプルな方法で計算しようと思う。
※この後①までは座標変換する場合「コンパス(3次元版 方針)」「コンパス(3次元版 実践編)」とやっていることは同じである。
生データを採取
まずは磁場と加速度データを採取する。

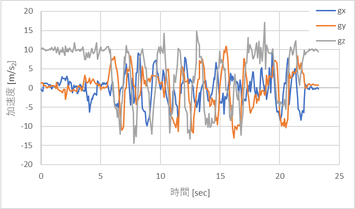
開始後5秒間くらいまでは水平にくるくる回し、その後いろんな方向に回した。
このデータを使うのだが、この後はこの中の1データを使って具体的に計算していき、最後に全体のデータがどうなってるか確認していこう。使うのは下記のデータにする。
Bo = ( 9.54 , -20.13 , -38.20 )
go = ( 0.80 , 7.45 , 3.50 )
Y軸方向に傾けた時のデータだ。
※出力(output)という意味で下添えのoをつけた。
①補正する
まずは「コンパス(2次元の場合)」でもやったようにスマホで計測した磁場Bo からゼロ点のずれを差し引いたBcを求める。スマホの磁気センサーというのは出力が多少オフセットしていることがあるのでこの操作が必要となってくる。2次元の時はスマホを水平にくるくる回したときのX、Yのそれぞれの出力を使ってゼロ点のズレを計算した。これは例えばX軸が磁北(全磁力の水平成分)方向に向いたときに最大の出力になり、磁北とは反対側に向けば最小の出力になることから、出力の(最大値+最小値)/2でゼロ点がどれだけずれているかが計算できるからだ。くるくる回していればY軸も同じように計算できるのは自明だろう。一方で3次元の場合で同じような考えでやろうとすると、全磁力に沿った向きにスマホの軸を合わせる必要が出てくる。全磁力がどっちに向いているかなんてわからない(わかっていたらコンパスなんていらない)ので、"なるべく"いろんな向きにスマホを傾けて、出力の(最大値+最小値)/2からゼロ点のズレを計算し、出力からズレを差し引くことで補正された磁場Bcを求める。
※"なるべく"というのが厳密でない感じがして気持ち悪いかもしれないが、これで妥協しても大きな問題にはならないだろうと考えている。なぜなら、全磁力Bとスマホの軸のズレをθとしたとき磁気センサーの出力はBcosθ+α(αはゼロ点のずれ)になるのだが、cosというのはグラフにすると頂点付近はなだらかなので、多少角度θがずれていてもcosθ~1だからだ。因みに25°くらいずれるとおおよそ1割ずれる。このくらいの精度でいいなら、"なるべく"でもいいだろう。
※水平面でくるくる回した後に、例えばX軸周りに回すでもいいのだが、そもそも水平面でくるくる回すことができるのであれば2次元の場合のコンパスで十分だ。
というわけでゼロ点のずれはスマホをぐるぐる回転させた時のBox、 Boy、 Bozの各成分の(最大値+最小値)/2で求められる。今回のデータ(計測した全データ)で計算すると
Box0 : 1.18 μT
Boy0 : 0.33 μT
Boz0 : 0.48 μT
のずれであった。これをBo から差し引けば補正後の磁場Bcが求まる。
Bc = ( 8.36 , -20.46 , -38.68 )
※補正が正しかったかは磁場の絶対値が一定になっていることを確かめればいいのだが、今回はズレがほとんどなかったので割愛する。(元からほぼ一定だった)
この後の流れは以下である。
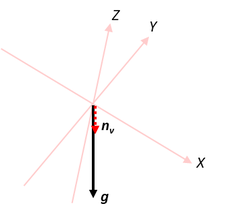
②加速度データから鉛直方向の単位ベクトルnvを求める
③nvとBcの内積を求める
(Bcの鉛直方向の成分の大きさが求まる)
④③で求めた内積の大きさをnvにかける
(Bcの鉛直方向の成分Bcvが求まる)
⑤BcーBcvを計算する
(地磁気の水平成分Bchが求まる)
地磁気の水平成分Bchこそが磁北の向きを示しているので、これでスマホに対してどっち向きに磁北が向いているか計算できたことになる。
早速具体的に計算していこう。
②加速度データから鉛直方向の単位ベクトルを求める
計算に使う加速度のデータは
go = ( 0.80 , 7.45 , 3.50 )
スマホをゆっくり動かした場合、加速度データのほとんどが重力加速度で占めていると考えられるので、この加速度ベクトルの向きと鉛直方向が一致していると考える。ただし注意が必要なのはこの加速度データは重力加速度の向きとは逆向きである。なぜなら加速度センサーは加速度そのものを計測しているわけではなく、中に入っている錘がセンサー素子を押す力を計測しているからだ。重力で錘が引っ張られるとあたかも反対方向に加速しているのと同じ出力が出てしまうのだ。なので、重力加速度のベクトルの向きは符号を逆にした
g = ( -0.80 , -7.45 , -3.50 )
になる。
絶対値g = √(gx2 + gy2 +gz2) = 8.27
なのでgをgで割れば鉛直方向の単位ベクトルnvが求まるので、
nv = g/g = ( -0.10 , -0.90 , -0.42 )
となる。
※nvの向きは上向きでも下向きでもいいのだが、なんとなく重力加速度の向きに会わせた方が直感的に思えるので、鉛直下向きにした。
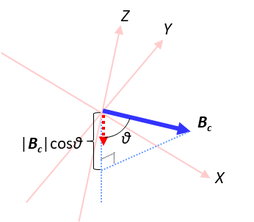
③鉛直方向のベクトルと補正後の磁場の内積を求める
nvとBcの内積を求める。これでBcの鉛直方向の成分の大きさが求まる。
具体的には
nv・Bc = |nv||Bc|cosθ
=|Bc|cosθ ( |nv| = 1なので)
となるのでBcの鉛直方向の成分の大きさになる。
実際に計算してみると、
nv・Bc = ( -0.10 , -0.90 , -0.42 ) ( 8.36 , -20.46 , -38.68 )
= 34.00
になる。
④内積の大きさを鉛直方向のベクトルにかける
③で求めた内積の大きさをnvにかける。これでBcの鉛直方向の成分Bcvが求まる。

Bcv = |Bc|cosθ × nv
= 34.00 × ( -0.10 , -0.90 , -0.42 )
= ( -3.28 , -30.63 , -14.40 )
⑤地磁気から鉛直方向の成分を差し引く
地磁気から鉛直方向の成分を抜けば残りは水平成分のみになるので、Bc ー Bcvを計算することで地磁気の水平成分Bchが求まる。

Bc ー Bcv = ( 8.36 , -20.46 , -38.68 ) - ( -3.28 , -30.63 , -14.40 )
= ( 11.64 , 10.17 , -24.29 )
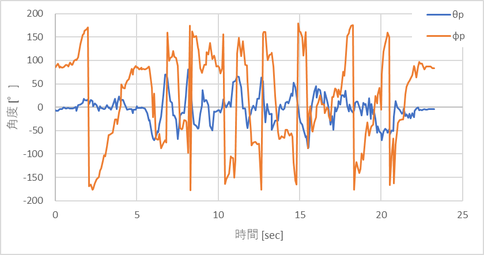
全データについて計算してみる
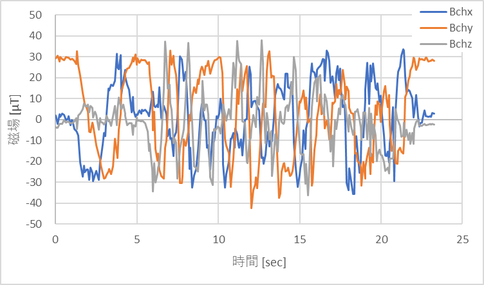
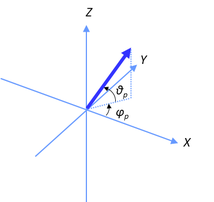
計算結果が上グラフである。当然と言えば当然なのだが、「コンパス(3次元版 実践編)」の計算結果と全く同じ結果となっている。あとはこれを極座標で表現してやれば磁北の向き(角度)がわかる。これも全く同じ結果であるが、再掲しておこう。
まとめ
シンプルと言いつつ長くなってしまったが、特に難しい計算もなく、直感的に理解できる計算のみで磁北を計算することができた。
一度理解してしまうと案外簡単なものだな。
(私はここにたどり着くのに紆余曲折したが)
