「遠心力」の実験でプラレールを使って検証を行ったが、理論値に近い遠心力がかかっていそうなことは確認できたものの、ノイズが大きすぎて本当に確認できたのか？と思いたくなる結果であった。

そこでやり方を一新して、再挑戦してみることにした。

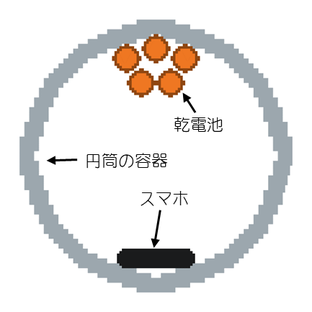
円筒の容器(タッパーのようなもの)にスマホをくくりつけて転がす。

円筒の外側に遠心力が働くはずなので、それをスマホで計測するという魂胆である。

※スマホをくくりつけるとその部分だけ重くなってバランスが悪くなるため、反対側に乾電池(図の茶色の円)をくくりつけてバランスをとっている。

(バランスウェイト)

上は実験装置(円筒の容器)を転がした時のZ軸方向にかかった加速度。

※遠心力がスマホのz軸方向にかかるようにスマホをセットした。

開始1秒後に転がし始める。それまでは10 m/s²くらいであったが、転がし始めると加速度が上下に波打ち、3秒後くらいに波打つのが止まる。波打つのが止まったのは壁にぶつかって回転が止まったため。つまり、回転しているのはこの波打っている部分だけである。

この波打っているのは一体何か？この実験の場合、遠心力のほかに重力加速度gの成分が加わっているであろうということは容易に推測がつく。つまり、

　加速度(生データ) = 遠心力 + 重力加速度の成分 ・・・(1)

となるだろうということ。そこで加速度(生データ)から重力加速度の成分を取り除いてみよう。

円筒容器がθ° 回転したとき、スマホのz方向にかかる重力加速度の成分は g cosθである。（下図）

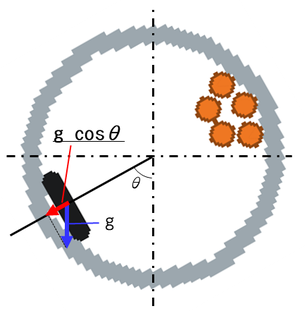
角度θはθ = ωt + φ （ω：角速度、φ：位相）であるから、ωとφを適当に調整してやれば、この波打っている部分を再現できるはずだ。そのωとφをいろいろ調整して生データに近い波形にした結果が↓（"重力加速度の成分"）。

上下で別れているが、同じ周期で波打つ波形をうまく再現できている。そして"加速度（生データ）"からこの"重力加速度の成分"を引いたのが"加速度（補正後）"で、ほぼ一定の値になる。これこそが遠心力である。

この実験ではω = 7.4rad/sでa = 4.7 m/s²だった。

ただこの数字は(1)から導き出したものだけれども、(1)はきっとこうだろうという仮定である。遠心力がどうかを確かめるには、ma = mrω²の関係に従うかどうかを確かめるのがいいだろう。そこで回転する速さを変えて転がして、上記の分析を繰り返せば、ωと遠心力の関係がわかる。

実際にやってプロットしたのが下図である。

（遠心力は"加速度（補正後）"で平らになっている部分から1秒分のデータを抜き出し平均値を算出したもの）

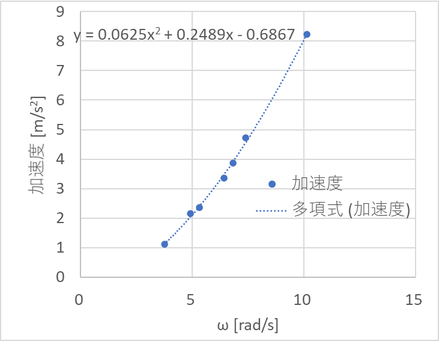
ωが大きくなるにつれて加速度も大きくなっていることがわかる。遠心力はωの二乗に比例するはずなので、2次式の近似曲線をグラフに追加してみた。かなり良く近似できていることがわかる。ただ、このままだと実は3次式でもうまく近似できてしまうので、本当に２次式かどうかはっきり言えない。

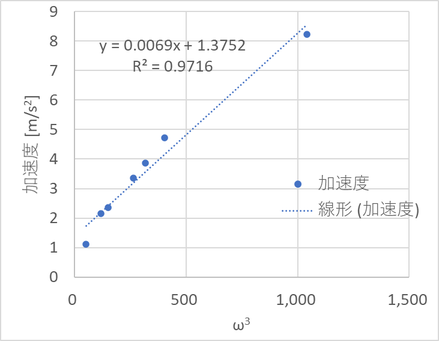
ということで、前回同様、横軸をω²でプロットする。（下図）

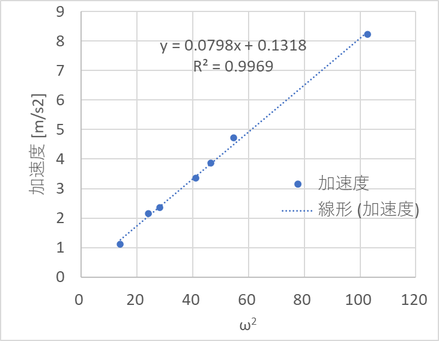
きれいに直線に並んだ。遠心力がωの二乗に比例することが確認できた！やはり、遠心力は a = rω²となるのだ。

そして今回の実験のやり方でうまく遠心力を計測できた！

<参考>

ちなみに横軸をω³にするとこんなにきれいに直線には乗らない。下図