「運動方程式」「運動方程式2」の実験では物体の加速度が力に比例することを多少のずれはあるものの確認することが出来たが、このときは台車の質量mを固定してFがaに比例することを確認する実験を行った。ただ運動方程式はF = maであるので、aを固定すれば、Fはmに比例するとも言える。

そこで今回の実験では質量mを変えて運動方程式を検証する。

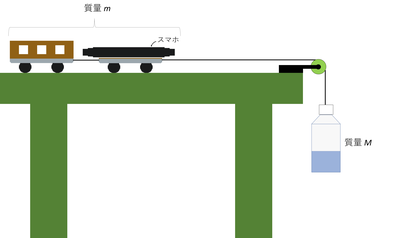
台車の上にスマホをのせ、水を入れたペットボトルと台車を紐で結ぶ。ここまでは「運動方程式2」の実験と同じであるが、台車の後ろにもうひとつ台車（台車2）を繋げる。2つ目の台車に錘(乾電池)をのせて台車側の質量を変えた。あとは台車を支えていた手を離すと台車は動き始めるのでその時の加速度を計測する。

※スマホのY軸を進行方向に向けた。この後出てくるデータはY軸方向の加速度である。

※スマホと台車及び台車2の質量をm、ぶら下げたペットボトルの質量をMとする。

手を離した後に台車は加速し、（ばらつきは大きいものの）一定の加速度になっていることがわかる。この一定になっている区間の加速度を一定時間抜き出して平均値aを出した。

(大きくマイナスの加速度にになっているところは台車をてで止めたときの衝撃)

これをmとMを変化させながら実験したときの加速度aが以下である。

mとMの組み合わせを変えれば当然加速度aが変化する。そんな中でも四角で囲ったデータはおおよそ同じ加速度になっている。

※なぜこんなにうまいこと同じになったかと言うと、そうなるように狙って組み合わせを計算したのだ。そう、運動方程式を使って。ん？求めたい結果を先取りして使っている？となるかもしれないが、これは特に問題ないだろう。たまたま得られたのか、狙って得られたのかの違いはあるが、得られたデータに特に仮定は入っていないのだから。(言い換えると最初から狙って組み合わせを考えるか、いろんな組み合わせを試行してあとから同じ加速度の結果を選ぶかの違いしかないと言うことを言いたい。)

この各枠内の加速度が同じと見なして、同じ加速度の時のmとMの関係を調べてみよう。

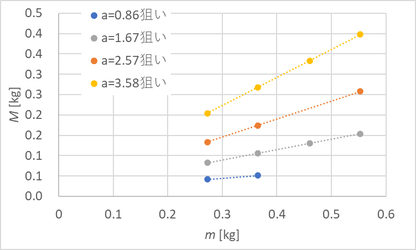
同じ加速度であればM ∝mになることがわかる。

当初の目的はFとmの関係を調べるであったので、最後にMをFに変換してやりたい。直感的にはFはMに比例するのだが、、、ここはしょうがないので「運動方程式2」の実験と同じように計算して求めよう。

　Ma = Mg - F

を使えばいい。

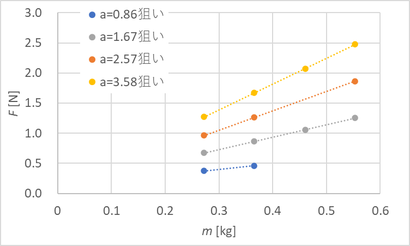
これでF はaを固定するとmに比例することが確認できた。

 上では同じ加速度になるように狙った時の結果をまとめてみるとF ∝mになることが確認できた。

といってもこのグラフのFを求めるのに使った加速度はあくまで狙い値である。実際には下図のように同じ狙いといえども、1回毎に加速度の値はばらついている。 

今回の場合、同じ狙いの時の加速度はそれほどばらついてはいないので、各狙い毎に加速度は同じだったと言っても大した問題はなさそうではある。が、どこまでばらついてもいいのかといわれると答えに困る。もう少しばらつきのある次のようなa = 1、m = 1の実験と、a = 2、m = 1の実験と、a = 1、m = 2の実験があった場合、どうやってグラフ化したらF = maをうまく表現できるだろう？縦軸をF、横軸をaとしたら1番目と2番目を比べることができるが、質量の違う3番目（下左図△マークの点）はどう比較したらいい？となる。一方で横軸をmにすると1番目と3番目を比べることはできるが、加速度の違う2番目（下右図◇マークの点）は比べられない。

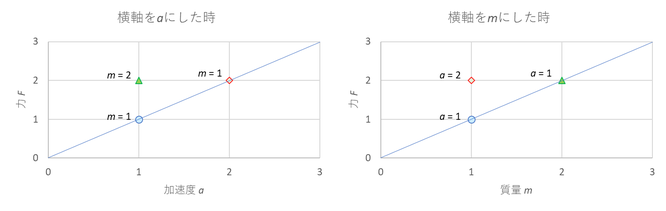
結局2つのグラフを用意して同じ質量、同じ加速度のデータで比べればいいのか？いや、mとaの組み合わせは無限にあるのに、その中から同じものを選んで比較したところで、ある限られた組み合わせでは比例するということしか確認できない。どんな組み合わせでも成り立つと言おうとしたら無限の数のグラフが必要になる。

では横軸をmaにしてみたらどうだろう。Fとmaは比例することがひとつのグラフで確かめることができるだろう。F = maなのだから当たり前でしょと思うかもしれない。でも実際にやってみるとその威力がわかるだろうから、最初のグラフの横軸をm→ma に変更してみよう。

ほら、一直線にならんだ。元のグラフでは(ほぼ)同じ加速度のデータでグルーピングしてやる必要があったが、このグラフであればどんな条件のデータでも一直線に並んでることからF がmaに比例することが一発でわかるだろう。

おっと、比例はするがF = maにはなっていない。これは「運動方程式2」でも出てきた台車の転がり抵抗だろう。同じように今回の結果から差し引いてやると以下のようになる。

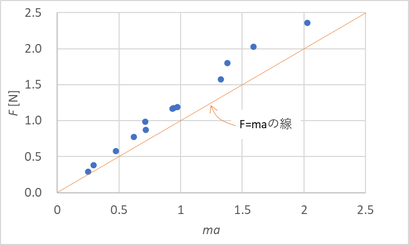
まだずれはあるが、とにかくF ∝ maであることはこのグラフから一目瞭然だ。ここで重要なのはmを固定してとかaを固定してとかの条件はないってことだ。

（こういう理論と実験のずれを解明していくと新しい発見があるのだろうけど、今回はここまでにしたいと思う。こういう大体あってればいいかみたいな姿勢が私がいまちな理由なんだろうな。余談であるが、、、）

どんな組み合わせでもひとつの直線で表されるのであるから、こっちの方が包括的な考え方と言えるだろう。そうなるとじゃあmaってなに？というのが気になってくる。F = maだから力のことだっていうのはわかっているのだが、maを変形してやると見え方が変わってくる。まず、

　a = dv/dt 

であるので、

　F = ma = m(dv/dt）

になるが、mは時間によって勝手に変化しないので(質量保存則)、微分のなかに入れることができて、

　F = ma = m(dv/dt) = d(mv)/dt

となる。おぉ、mvって運動量pのことじゃないか！つまり、

　F = dp/dt

ということだ。つまり力とは運動量を変化させるもののことなのだ。

※もし微分を習っていない人がこれを見ているとしたら．．．

dx （xはvとかaとかの物理量）というのは変化量だと考えてもらえればいいと思う。dvだったらvが変化した量、daだったらa、d(mv)だったらmvの変化量という意味。それを変化が起きた時間dtで割ったということ。ただ注意点としては、途中でm（dv）＝d（mv）とする式変形をしたがこれはmが定数であるからできることで、mが定数でない場合はそうならない点だ。

<蛇足>

F = dp/dt であることを確認できたがこれを質量保存則を仮定せずに微分してみよう。

　F = dp/dt = d(mv)/dt

積の微分を使えば

　　= v dm/dt + m dv/dt

　　= v dm/dt + ma

となる。

F = maにv dm/dtが足される。こうなると質量が保存されない世界ではF = dp/dtと習うことになるのだろう。(勝手な想像だが)