運動方程式2
目次
<やり方>
装置の配置
力Fの計算方法(今回の実験では力Fを計算で求める)
<結果>
加速度データからペットボトルに引っ張られている間の平均加速度を求める
ペットボトルの質量Mを変えて、質量M vs 加速度aの関係を調べる。
質量Mから力Fを計算し、力F vs 加速度aの関係を調べる。
(→F = maであることが確かめられる)
<F=maを示せたか?>
計算値とのずれを転がり抵抗によるものと仮定し、転がり抵抗f を求める。
求めた転がり抵抗をもとに力Fと加速度aを計算し、力F -f vs 加速度aの関係を調べる。
(→より正確にF = maであることが確かめられる)
<卵が先か、鶏が先か>
力F を計算で求めたことについての考察。
<おまけ(勘違いしたこと)>
計算値のずれを考察するうえで勘違いしたことを備忘録として記載
やり方

台車の上にスマホをのせ、水を入れたペットボトルと台車を紐で結ぶ。台車を手で支えながら滑車を介してペットボトルをぶら下げる。支えをはずすと台車は動き始めるのでその時の加速度を計測する。
※スマホのY軸を進行方向に向けた。
※スマホと台車の質量をm、ぶら下げたペットボトルの質量をMとする。
ここで今回の実験でどのような力Fが台車にかかるか説明しておこう。というのも今回実験に使った装置のなかに力Fを測定するものがないので、計算で求めたからだ。
台車側質量はmで、力Fがかかるので、台車側の運動は
ma = F
となる。一方でぶら下がったペットボトルの運動は
Ma = Mg - F
となる。(ペットボトルに働く力は重力で引っ張られる力Mgと紐で引っ張られる力F。紐で繋がってるので、台車と同じ加速度aで動く。)
この2つの式からFを求めればよく連立方程式を解けば、
F = mMg/(m + M)・・・(※)
となり、mとMがわかれば計算できるので、今回の実験では力Fをこの式から求める。
(aは上式をmで割れば求まる)
※運動方程式が本当に成り立つか確認する実験なのに、前提条件として運動方程式を使っていたら、鶏が先か卵が先か状態になるじゃないか、、、と言われそうだ。それはその通りであると思うが、言い訳は下に書く。
結果
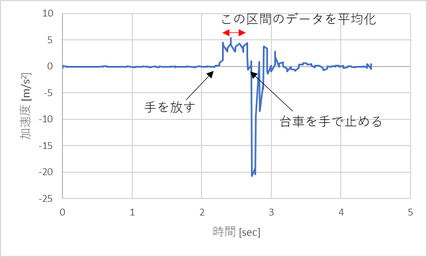
まずは運動中の加速度の推移から。手を離した後に加速し、(ばらつきは大きいものの)一定の加速度になっていることがわかる。これが今回知りたい加速度である。(その後波形がぐちゃぐちゃになっているのは台車を止めようとしたときのもの)
ペットボトルの水の量を変えれば引っ張る力が変わるので、加速度も変わるだろう。そこでペットボトルの水の量を変えて、その時の加速度をプロットしたのが下図。(引っ張られてる区間の加速度を一定時間抜き出して平均値を出した)

ペットボトルの質量が増えるにしたがって加速度が大きくなっている。ただし直線ではなく、上に凸の曲線になっている。なぜなら横軸はまだペットボトルの質量Mであるからだ。
そこで(※)式から、力Fを計算してグラフ化してみよう。(台車側の質量mは0.3㎏であったのでそれを入力している。)

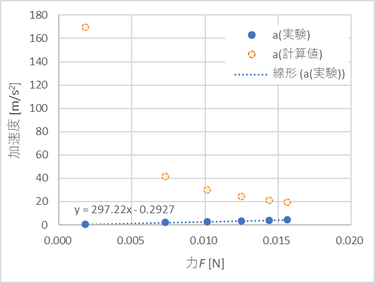
青プロットが今回の実験結果であるが、直線になっている。(横軸が力Fなので、a = (1/m) Fの関係になっている。)
青点線が1次式で近似した線であるが、傾きは質量の逆数である。1/m = 3.084 ということはm = 0.324 kgであり、実際の台車側の質量m = 0.3にかなり近いことがわかる。
F = maを示せたのか?
とここまで書いては見たものの、全体的に計算値よりも小さい加速度になっている点が気になる。全体的に下がっているので測定時のばらつきによる誤差ではなさそうなんだよな。何か原因がありそうだ。
パッと思い付くのは台車の転がり抵抗か?そこで、ペットボトルが取り付けてあったところに硬貨をぶら下げて、何グラムで台車が動き始めるかを確認してみた。結果は8.5g分の硬貨をぶら下げると台車が動き出した。つまりこの台車は8.5gf = 0.083Nの転がり抵抗がありそうだ。
この転がり抵抗をfとすると台車とペットボトルの運動は以下のように書き換えられる。
ma + f = F
Ma = Mg - F
この2つの式から
F = m ( Mg - f ) / ( m + M ) + f
a = ( F - f ) / m
となるので、計算しなおしてみると以下のようになる。
※横軸はF - f にした。台車はこの力で加速することになるはずなので。

力が大きい時にずれはあるものの、最初の転がり抵抗を考慮していないときに比べてかなり一致した。
あと一歩という感じがしないでもないが、F = maが成りたっているとと言っていいだろう。
卵が先か、鶏が先か
" いや、運動方程式が本当に成り立つか確認する実験なのに、前提条件として運動方程式を使っていたら、鶏が先か卵が先か状態になるじゃないか、、、と言われそうだ。"と書いた件。
じゃあどうやればよかったかというと、例えば台車とペットボトルを結ぶ紐の途中にバネばかりを仕込んで力を計測しておけば、運動方程式を使わずにすんだだろう。ただし実際にやろうとすると大変である。重いから垂れ下がるだろうし、なにより運動している間にバネがどれだけ延びていたかを正確に計測しようなんて無茶だろう。なので、Fの値は計算値を使わせていただくことにしたのだ。
ただ途中で結論を仮定していれたら、結果がその通りになるんじゃないかという疑問はそのままだ。つまりF = maのFにmaを代入してma = maみたいなことをしていないかって言う心配だ。そこで、例えばF = ma2だったらどうなるか?みたいなことをやってみよう。こう仮定して計算しても実験の結果と辻褄があってしまうのであればma2 = ma2のようなことをやってしまってるのだろう。F = ma2だとしてF、aを計算すると
F = (Mm/(m+M)) g2
a = √(M/(m+M)) g
となる(※転がり抵抗は考慮していない)。これを使って実験結果をプロットしたのが以下。

実験と計算結果が全く一致しない。
別のパターンとしてF = m/aだとしてグラフ化したのが以下で、これも全く一致しない。(※ここも転がり抵抗は考慮していない)
どうやらma = maのようなことはやっていないようだ。これはFとaを独立して計算できているからだろう。
上記を総合して考えてみるとF = maを発見することはできないけれど、F = maだと仮定すれば実験結果を説明できるというのがこの実験の位置付けだといっていいだろう。
おまけ(勘違いしたこと)
計算値と実験値がずれていたことに対する考察で、実は次のようなものも考えていた。途中で間違いだったことに気づいたけど、備忘録として残しておこう。
今回実験値のほうが加速度が小さくなるほうにずれていたのだけれど、それはペットボトルの中の水が落下に追従できずに浮き上がったせいで、紐を引っ張る力Fが小さくなったためなのではないかと。

これは簡単に間違いだとわかる。(のだけれど、私は勘違いした(汗))仮に水が分離したとしたら分離した水は重力加速度gで落下することになる。一方で、ペットボトルは紐に力Fで引っ張られているので、ペットボトルが落下するときの加速度aはgより小さくなるはずだ。だから分離なんてしないことがわかる。
