運動方程式
F = ma
古典力学のもっとも基礎的な法則のひとつである。物体の質量が重いと動かしにくいし、物体に大きな力をかければかけるほど加速するだろうから、この法則が成り立つだろうことは何となくイメージ出来る。
でも実際に成り立っているかどうやって確かめるか?
F はバネを使えばよい。(フックの法則)
m は秤を使えばよい。
a は、、、加速度センサーがある!
ということで、運動方程式を確かめる実験をしてみた。
※スマホの加速度センサーって原理的には運動方程式を使って力から加速度を出してるんだから、運動方程式が成り立つ前提で実験していることになっていないかという疑問が出てきそうだ。これについては、「本当に加速度を計測できているのか?」の実験でセンサーから出力される値は加速度であろうことは確かめているので、測定原理には目をつぶって加速度を計測するものとして使っても問題ないだろう。
やり方
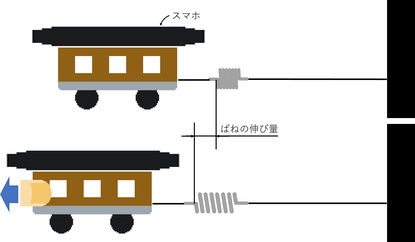
ぷらレールの貨車にスマホを載せる。その貨車をバネにつなぎ引っ張り、伸び量を確認した後に手を離す。
※スマホのY軸を進行方向に向けた。
※この実験では加速度データのサンプリングレートをFASTEST(計測できる最速の間隔)で計測した。
結果
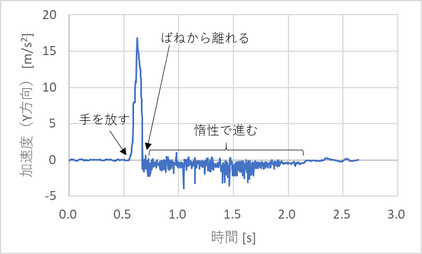
まずはバネに引っ張られたときの加速度を見てみよう。引っ張った状態で計測をスタートし、0.5秒後くらいに手を離す。離した直後にバネに引っ張られて加速度が跳ね上がる。その後すぐに加速度が小さくなり、ほぼゼロになる。ほぼゼロといったがよく見るとややマイナスである。バネで引っ張られなくなり、惰性で進んでいる区間で、転がるときの抵抗によってだんだん速度が低下していっているところである。そして最後に停止し、加速度がゼロになった。
さて、今回は運動方程式F = maを確かめたいのであるが、一体どの部分のデータを使えばいいのだろうか?mは変化することはなく、aはずっと記録していたので、後はFさえわかれば確かめられそうだ。この実験では手を離したときのバネの伸び量を確認しているので、フックの法則から手を離した直後にかかっている力Fはわかる。そして手を離した直後の最大加速度がその力Fで引っ張られたときの加速度であろう。ということで次に上記の実験をバネの伸び量を変えて繰り返してみた。

その結果が上であるが、バネの伸び量が増えるにしたがって加速度も大きくなる。しかも直線的に。いい感じではあるが、伸び量がゼロの時に加速度がゼロにならなさそうだ。
これは実験で使ったバネに特徴があったためだ。使ったバネは伸び量がゼロの時にも力がかかってるタイプのバネを使ったためである。普通フックの法則は F = kx と表されるけど、このバネは F = kx + α の力がかかるものであったのである。
そこで横軸を力に変換してやればグラフの原点を通る運動方程式の関係が得られるだろう。ということで次にバネの伸び量と力Fの関係を調べた。(今回の実験の目的から少しずれるので興味のない方はこの部分を読み飛ばしてもらって構わないと思う)
<バネの伸び量と力の関係>
バネにペットボトルをぶら下げて、ペットボトルのなかに水を入れていき、ペットボトルの重さとバネの伸び量を確認した。
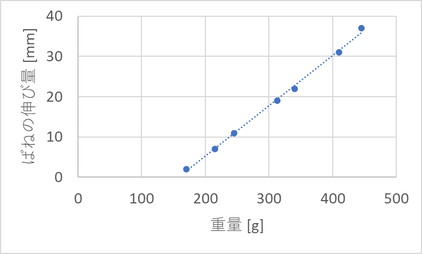
上で述べたように伸び量がゼロの時にも力がかかってるため、150gくらいでようやくバネが伸び始めていることがわかる。
このバネが従うフックの法則 F = kx+α のkとαを求めるには、グラフの縦軸と横軸を入れ換えて、重量を力に変換する。(重量のgをkgにして、重力加速度をかければNに変換できる。)
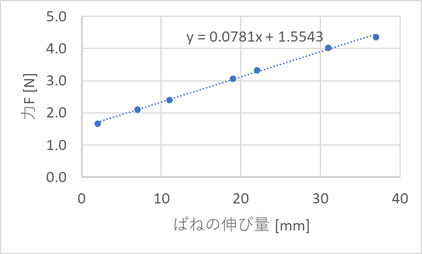
この結果から今回実験に使ったバネの伸び量xと力の関係Fは
F = 0.0781x + 1.5543
であることがわかる。
上記からバネの伸び量を力に変換した結果が下図である。
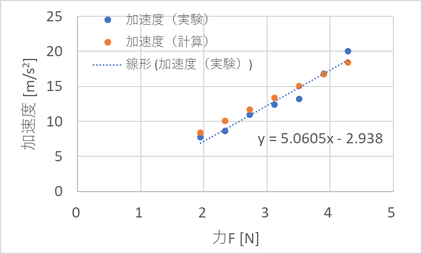
青丸プロットが今回の実験値であるが、ほぼ直線に乗っている。そして一次式で近似したのが点線である。運動方程式を変形するとa = (1/m) Fとなり、このグラフの傾きは質量mの逆数となるので、 (1/m) = 5.0605 → m = 1/5.0605 = 0.198 kgと計算される。実際の質量0.233 kgだったので、結構近い数字が得られた。またオレンジ丸プロットはバネの伸び量から計算した加速度の結果であるが、かなりよく一致していると言えるだろう。(差は6%)
今回の実験でF = maとなることはある程度確認できたと言えそうだ。
課題
上では都合のよい結果を並べて、F = maであることを確認できたと書いてみたものの、今回の実験はあまり完璧とも言えないところがある。
まず、力と加速度のグラフ(最後のグラフ)で近似線が原点を通っていない。荷重がゼロの時に-2.9 m/s2くらいの加速度になってて、今回の実験結果に対して無視できないような大きさになった。この原因は恐らく0 N付近の力での結果が少ないせいだと思う。(得られたデータ範囲より外側を予測しているため)
次はバネの伸び量の測り方。今回の実験ではバネに定規を当てて測ったのだけれど、当然1mm単位でしか測れなかったし、片手でぷらレールの貨車を引っ張りながらもう一方の手で定規をバネに当てながらの状態で読んでたので、かなり誤差が大きかったと思われる。
最後に手を離した瞬間っていうのがどこであったかはっきりしないこと。最初ののグラフを見ると、加速度が急増しているところが手を離したところであるのはわかるものの、よく見ると少し傾きをもってだんだん加速度が増加していくのがわかる。瞬間的に手を離せていれば、瞬間的に加速度も上がっていたはずである。今回の実験では瞬間的に手が話せていなかったのであろうと思われるが、そうなると最大加速度が得られた時点ではすでに少しバネが縮んでしまったあとであると考えられる。実際に最後のグラフで多くのプロットが計算値より小さいのはそのためではないかと思われる。
ということで課題が多い実験だったので、実験のやり方を改良して再チャレンジしてみたいと思う。
余談
書きたかったけど、本文に入れれなかったことを、ここで供養しておく。
<歴史的な経緯>
ニュートンは一体どこからこの法則にたどり着いたのだろうか?精密に時間を測ることもできなかったはずの当時に加速度なんて簡単に測れそうになさそうなのだが。加速度って定義は単純だけど、それを測るのはなかなか大変だ。
単純に思い付くやり方はA、B、Cの3地点を通過する物体のそれぞれの通過時刻を記録するやり方だろう。AとBの通過時間からその間の速度が計算でき、BとCの通過時間から、、、とやってけば計算できるだろう。だが、通過時間をどれだけ正確に図れるかはなかなか難しい課題じゃないだろうか。1秒単位だったらストップウォッチでなんとか行けそうだが、0.1秒、0.01秒になってくると怪しい。しかも3地点となると同じ時計で3回連続測るか、正確に時刻合わせした3つの時計を使うかになって、それもひとつのハードルになりそうだ。
どうも歴史的には、ガリレイの巧妙な実験からこの法則にたどり着いたようである。その実験とは斜面の上を球体を転がす実験である。斜面には鈴を何個かつけ、球体が通過すると鈴が鳴る仕掛けになっている。鈴が等間隔で鳴るように配置すれば時間と距離の関係がわかるというものだ。(豊田利幸「物理とは何か」岩波書店 2000)
いや、ガリレイって本当に天才だなって改めて思うな。
<法則か定義か>
運動方程式は運動の第2法則の中にある。力も質量も感覚的には馴染みのあるものなので、それにa = d2x / dt2で定義される加速度も加えた3つの物理量の間に成り立つ関係式と考えれば法則といっていいだろう。でも、力と質量って正確にどうやって定義されるのだろうか?実は運動方程式で力と質量の定義しているのだ。力とはある物体の加速度を変化させるのに必要なもので、加速度に比例するもの。その力で物体を加速させたときの加速しにくさが質量と定義される。
教科書でこの関係式が成り立つ実験結果って見たことないなと思っていたが、定義つまり決め事なので、いつでも成り立つはずだから実験も必要ないってことかな。
にしても、その定義が妥当かどうか体感するような実験はあってもいいと思う。
、、、おぉ、このページにうってつけの実験が載ってるじゃないか!
