ぷかぷか浮いている風船。浮いているのは浮力のおかげのはずだ。

いきなり何を当然のことをと思われるかもしれないが、今回は風船が浮力(気圧差)で浮いていることを確かめたい。

なぜこんなことをしたいかと思ったのは以下の理由だ。

まず気体・液体の中にいれた物体には浮力が働き、その浮力の大きさは物体の天面と底面にかかる圧力差で決まる、と習った。

下図は水の中に入れた容器の模式図である。水圧は水深に比例するので、天面にかかる圧力(緑矢印)と底面にかかる圧力(赤矢印)に差ができ、底面側の方が力が強いため、上に向かって力がかかる。

水の場合は、日常的な感覚で水圧の大きさを考えると確かにいろいろなものが浮きそうだとイメージできる。 

では空気の場合は？風船にかかる浮力も気圧の差のお陰なのだろうか？

というのも風船の上半分にかかる気圧(緑矢印)と下半分にかかる気圧(赤矢印)にそんな大きな差があるなんて私にはあまり実感がわかない。

原理的には気圧差があるんだろうけれど、そんなのちっぽけなもんだろ、ちょっとした気圧の揺らぎに埋もれてしまうような差しかないんじゃないか、そんなので本当に風船が浮くのか？と言うのが正直なところである。

前置きが長くなったが、そんな疑問から風船くらいの大きさでもちゃんと気圧差があるか確認してみた。

20cmの高さの台の上と下で気圧を測定。

（20cmというのは風船の大きさを想定した高さ。少し小ぶりか？）

まずは台の上に置いて気圧測定開始。1016.70～1016.74hPaの間をばらついている。次に開始７秒後に台の下にスマホを降ろすと、1016.73～1016.77hPaの間をばらつくようになった。

台の上の時と下の時のそれぞれのデータをヒストグラムにしたのが↓

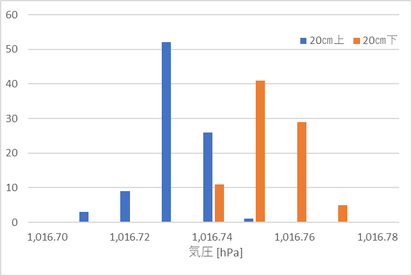
分布が明らかに別れており、高さによって気圧が変わったと言えるだろう。(他に変化点と呼べるようなものはない)

平均値は

　台の上の時：1016.7265±0.0007 hPa

　台の下の時：1016.7481±0.0008 hPa

となった。

※平均値の誤差が小さいのは90個近いデータを使って計算したため。

その差は0.0216hPa = 2.16Pa

確かに気圧差はある。、、、だが、2.16 Paってどのくらいの大きさだ？

2.16 Paあれば風船が浮きそうだなという実感がまだわかないな。

ということで次にこの結果を使って浮力を求めてみよう。やはり力にしないと実感がわかないので。例えば20cm×20cm×20cmの立方体の場合はどのくらいの浮力になるか。(風船って大体こんな大きさだろう。ちょっと小さめか？) 

天面（=底面）の面積は0.04m²だから、

浮力 = 気圧差 × 面積 = 2.16 × 0.04 = 0.086 N = 0.009 kgf

となる。つまり9gだ。一円玉9個分。

当初は風船くらいの大きさで発生する気圧差なんて外部要因ですぐにかき乱されてしまうようなちっぽけなものであろうと思っていたのだけれど、2.16Paというのははっきりと実感できる浮力を発生させられるのだ。

おぉ、全然ちっぽけな差ではなく、ちゃんと気圧差で浮いていた！

次の実験では空気の密度を調べて見たいと思う。

唐突に空気の密度が出てきたけれど、この実験をまとめていて、気圧差のデータを使えば空気の密度が計算できることに気づいたので、せっかくなので計算してみようと思った次第だ。

乞うご期待