スマホの加速度センサーを記録するアプリを作ってみたけれど、そもそもスマホの加速度センサーから出力される値は本当に加速度なのか？スマホを動かさないで放置していると10 m/s²くらいの数値が表示され、重力加速度9.8 m/s²に近い数字なので確かに加速度を表示してるっぽい。でもそれっぽい数値というだけだ。たまたま同じような数字の全く加速度とは関係のない数字を出力しているだけかもしれない。（もちろんたまたまという可能性は低いと思っているが。）

加速度の定義に立ち返れば、単位時間辺りに進む距離が速度、単位時間辺りに増加する速度が加速度であるから、加速度がわかれば進んだ距離を逆算できるはずである。

この方法でスマホの加速度センサーが実際に加速度を計測しているのか確認してみた。

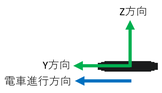
電車にのって、スマホのY方向を電車の進行方向に向けた状態で置き、加速度の計測を実施。

一駅間の加速度データを保存。（話を単純化するためほぼ直線の区間にした。）

計測した加速度から以下のようにして進んだ距離を計算する。

　1.計測した加速度と時間のデータから速度を計算

　2.その計算した速度と時間のデータから距離を計算

　(具体的な計算のしかたは後述する。)

最後にその計算結果と実際の進んだ距離と比較する。

上が加速度の計測結果。（Y方向の加速度）

５秒後くらいに出発。30秒くらい加速して、その後惰行運転に切り替わった。60秒後くらいにブレーキを掛けはじめて、90秒後くらいに次の駅に到着。

これだけだと、ただ単に私の乗った区間がこんな感じで運行してるんだなというだけ。

次にこの加速度から速度を求めてみよう。加速度を積分してやれば速度になるはずだ。

<加速度→速度の求め方>

ある瞬間の加速度をa_i、次のデータまでの時間間隔をΔtとすれば、Δt の間の速度の増加分をΔv は、

Δv = a_i Δt　・・・(1)

となる。だからこれを採取したデータすべてで計算して足していけば速度が求まるはずだ。

ただ、加速度はこんなにカクカク変化するのではなく、もっと滑らかに変化してると考える方が自然だろう。

そこで下図のようにプロットとプロットの間は直線的に変化したと近似する。そうすると、速度の増加分Δvは２点の平均値を使って

Δv = (a_i+1 + a_i ) 2 Δt　・・・(2)

となって、これを足し合わせていけばvを求めることができる。(台形積分。詳しくはweb検索で)

この台形積分を使って加速度→速度の計算を行った。

結果が↓

速度は5秒後くらいに上がり始め、15秒後くらいでピークに。その後、惰行運転に切り替わったところから徐々に速度が低下し始めて、ブレーキを掛けはじめたところから一気に減速。ちなみに15m/sというのは大体55km/hなので、最高速度としてはまぁイメージと掛け離れてはいないかなというところ。

次の駅に着いた時に速度がゼロになってないのは気になるところだがそれは後述するとして、その前に距離の計算結果を見ておこう。なぜなら今回のゴールは計算した距離と実際の距離を比較することで、加速度が測れているか確認することだからだ。

距離はもう一回台形積分してやれば求まるはずだ。(上では加速度→速度の計算を例に説明したが、加速度を速度、速度を距離と置き換えればそのまま使える)

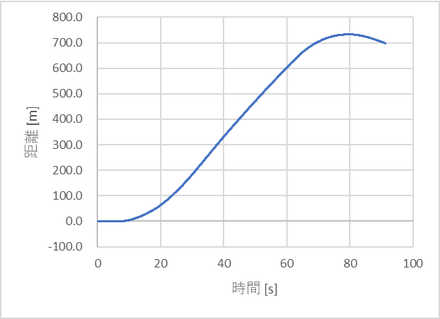
開始5秒後くらいに移動開始し、次の駅に到着した90秒後くらいには約700m進んだ計算になった。

 今回実験に使った区間の実際の距離は880m。

ということは私のスマホの加速度センサーの精度は誤差20％ってところだろう。誤差でかいな。

上記でやっぱり気になるのは、次の駅に着いた時に速度がゼロになってないところだろう。

90秒後に駅に停車したのは間違いないので速度はゼロになってなきゃおかしい。

20％の誤差って結構大きいし、もうちょっと精査してみてもいいんじゃないかと思う。

実は加速度のところで思い当たるところはあって、スタート時、停車時の加速度が僅かにマイナスになっている。常にマイナスの一定値が成分に含まれていて、それを積分していたら、速度はゼロに戻らずにマイナスになってしまうのは当然だ。こうなる原因としてはスマホを完全に水平に置いて計測できていないことが考えられる。水平に置けていないことで、Z軸にかかっている重力加速度の成分がY軸に乗ってきてしまっているのだ。

そこで傾いていると仮定して、データを補正してみよう。

…とその前に、スマホの加速度センサーがどのように加速度を検出しているか、説明が必要だ。

スマホの加速度センサーはピエゾ抵抗方式というものが一般的なようだが、これは錘に繋げたバネの変位をピエゾ抵抗素子の抵抗値で検出するという仕組みだ。(詳しくはWebで)

ここで仕組みを説明したのは、これから説明で使う模式図、数式はスマホの加速度ではなく、この錘がバネを引っ張る(押す)力で説明していることを明確にしたいから。そうしないとこの後出てくる模式図や数式の辻褄が合わなくなるのだよ。

※そもそもスマホを動かさないでそっと置いておくだけでも10 m/s²くらいの数値が表示されるのだから、スマホ自体の加速度そのものを表していないことは明かなんだけど。

前置きが長くなったけど、傾きを加味して補正するのにこの錘にかかってる力で考えることにする。錘にかかってる力を図示したのが下図。

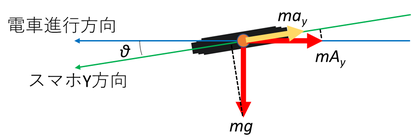
電車の加速度を大文字のA、スマホの加速度を小文字のa、電車に対してのスマホの傾きをθとしよう。そうしたときにスマホの加速度センサーの錘(質量m)がy方向にバネを引っ張る力は

ma_y = mA_y cosθ - mg sinθ

となる。

ここで電車が止まっているときは、

a_y = 0 - g sinθ

である。また今回計測したデータから電車が止まっているときはa_y = -0.05であるから、式に代入すると、0.3°ほど傾いていたようだ。

上記を使えば、肝心の電車の加速度は

A_y  = (a_y + g sinθ ) cosθ

　 =(a_y + 0.05) 0.99947

で求まる。

その結果が以下。

ちゃんと次の駅に着いた時に速度がゼロになっている。そして距離は約910mでおおよそ3％の誤差となった。

おぉ、なかなかの精度だ。

本来ならX方向もちゃんと加味しておくべきだろう。実際、Y方向は停車中も0.05 m/s²くらいの加速度がかかっていたのだけれども、これは水平におけていなかったから重力加速度が乗ってしまったためだろう。ましてや進行方向にX軸を直角におけていただなんて思えない。だからX軸も加味して、、、

なんだけれども、実際には電車が出発してから加速度が周期的に増減していて(これは電車が横揺れしてる加速度だと思われる)、こんなのを含んだまま計算したらきっとおかしなことになる、ってことで計算していない。

(、、、まぁ本音は計算が大変そうで億劫になってるだけだけど。)

あとY軸の加速度が停車中にゼロになっていないのを傾きと仮定して補正したけれど、一方で単純にセンサの基準（ゼロ点）がずれているっていう可能性も考えられ、どっちが正しいか検証できていない。

(ゼロ点がずれている = 水平に置いてもゼロでない値が出力される)

この辺りもう少し検証の余地ありだけど、スマホのセンサーが突拍子もない値を出力している訳でもなさそうなので、今回はこの辺で終わろうと思う。